Analog of Lusin’s conjecture for orthogonal polynomials from Szego class

December 24, 2019 in Uncategorized | 1 comment

The celebrated Carleson theorem for trigonometric Fourier series solved positively the Lusin’s conjecture. It says, in particular, that for every f\in L^2(\mathbb{T}), the Fourier series

\sum_{n}\widehat f_ne^{in\theta}

converges for a.e. \theta\in \mathbb{T}.

This results follows from the estimate on the Carleson’s maximal function. In the preprint with R. Bessonov, we studied the analog of Lusin’s conjecture for polynomials orthogonal on the unit circle.

Suppose \mu is probability measure on \mathbb{T}. It belongs to Szego’s class if \log \mu'\in L^1(\mathbb{T}). This class plays crucial role in many branches of classical analysis and probability (see other posts). If \mu is in Szego’s class, we can define Szego’s function by the formula

D(z)=\exp\left( \frac{1}{2\pi } \int_{\mathbb{T}} \frac{1+\bar\xi z}{1-\bar\xi z}\log \sqrt{ \mu'(\theta)}d\theta\right),\, \xi=e^{i\theta}\,,z\in \mathbb{D}.

Denote the polynomials orthonormal with respect to \mu by \{\phi_n(z,\mu)\}. The analog of Lusin’s conjecture says:

For \mu in Szego’s class, prove that \sup_{n}|\phi_n(z,\mu)|<\infty for a.e. z\in \mathbb{T}.

We were not able to solve this problem but we proved a few results that reformulate pointwise convergence of polynomials in different terms. Each measure \mu generates the sequence of Schur functions (analytic contractions on \mathbb{D}), that we denote by \{f_n(z)\}. Given a parameter \rho\in (0,1) and a point \xi\in \mathbb{T}, define the Stolz angle S_\rho^*(\xi) to be the convex hull of \rho\mathbb{D} and \xi. Our central result is the following theorem

Theorem.

Let \mu be Szego measure and Z(\phi_n) = \{z \in \mathbb{D}: \; \phi_n(z) = 0\}. Take any a>0 and denote r_{a,n}= 1-a/n. Then, for almost every \xi\in \mathbb{T}, the following assertions are equivalent:

(a) \lim_{n \to \infty} |\phi_{n}^{*}(\xi)|^2= |D_{\mu}^{-1}(\xi)|^2,

(b) \lim_{n \to \infty} {\rm dist}(Z(\phi_n), \xi)\,n = +\infty,

(c) \lim_{n \to \infty} f_n(r_{a,n}\xi) = 0,

(d) \lim_{n\to \infty}\sup_{z\in S_\rho^*(\xi)}|f_n(z)|=0 for every \rho\in (0,1).

The idea of the proof is based on the analysis of new entropy function which generalizes the standard Szego entropy. This quantity is well-behaved for a.e. boundary point and this gives uniform in n control over the oscillation of f_n(z) in z on the circle.

 

 

 

 

 

 

Spectral characterization of measure with finite logarithmic integral

March 13, 2019 in Uncategorized | Leave a comment

Roman Bessonov and I uploaded a new paper titled “de Branges canonical systems with finite logarithmic integral” to arxiv today. This is a continuation of an earlier manuscript, see also the previous topic on “Szego theorem on the real line and Krein strings”. In the current version, we completed the project of describing the measures on the line with finite logarithmic integral.  Assume \sigma is Poisson-finite measure, i.e., that

\displaystyle \int_{-\infty}^\infty \frac{d\sigma}{1+x^2}<\infty.

We define its logarithmic integral as

\displaystyle \int_{-\infty}^\infty \frac{\log \sigma'}{1+x^2}dx.

Existence of logarithmic integral, i.e., condition

\displaystyle \int_{-\infty}^\infty \frac{\log \sigma'}{1+x^2}dx>-\infty

plays a role in the theory of Gaussian stationary stochastic processes: it holds if and only if the future of the process with spectral measure \sigma can not be predicted by its past.

Every Poisson-finite measure \sigma gives rise to a function m in Herglotz-Nevanlinna class, i.e., the class of functions analytic in \mathbb{C}^+ with non-negative imaginary part, by a Herglotz formula

\displaystyle m(z)=az+b+\frac{1}{\pi}\int_{-\infty}^\infty \left(\frac{1}{x-z}-\frac{x}{1+x^2}\right)d\sigma,

where a\ge 0, b\in \mathbb{R}. The de Branges theory of Hilbert spaces of functions of exponential type provides a bijection between Herglotz-Nevanlinna class and the class of all canonical Hamiltonian systems. Canonical Hamiltonian system can be written as the following Cauchy problem

JM'=zHM, \quad M(0,z)=I_{2\times 2}, \quad J=\left( \begin{smallmatrix}0&-1\\1&0\end{smallmatrix}\right), z\in \mathbb{C}

where 2\times 2 Hamiltonian H(t) is nonnegative locally summable matrix-function on [0,\infty). In short, the Weyl-Titchmarsh theory for canonical systems provides m for each H and the converse is true by de Branges theory. In the paper, we characterize all H for which the logarithmic integral of \sigma exists. Consider H for which \sqrt{\det H}\notin L^1(\mathbb{R}^+). Then, define the grid of points \{\eta_n\} by the formula

\displaystyle \eta_n=\min\{t: \int_0^t \sqrt{\det H(\tau)}d\tau=n\}

and consider the quantity

\displaystyle K(H)=\sum_{n=0}^\infty \left(\det\left( \int_{\eta_n}^{\eta_{n+2}} H(\tau)d\tau\right)-4\right).

Our main theorem, which is stated below, is a natural generalization of the Szego theorem in the theory of polynomials orthogonal on the unit circle.

THEOREM. The measure \sigma has finite logarithmic integral if and only if K(H)<\infty for H generated by \sigma.

We quantify it by the sharp two-sided estimate. The sum in the definition of K(H) can be written in the form reminiscent of the matrix A_2 Muckenhoupt condition but we do not understand yet how the problem is connected to Muckenhoupt classes.

There are multiple applications of our theory to scattering problems for Dirac and wave equations.

 

 

 

ICM in 2022

September 12, 2018 in Uncategorized | Leave a comment

Jacobi matrices on trees and multiple orthogonal polynomials

June 18, 2018 in Uncategorized | Leave a comment

August 18, 2020. Two preprints were submitted lately. One is “Jacobi matrices on trees generated by Angelesco system: asymptotics of coefficients and essential spectrum” with A. Aptekarev and M. Yatselev. For Angelesco system with two real-analytic weights, we performed the Riemann-Hilbert analysis to obtain asymptotics of polynomials of the first and second type when the multi-index n=(n_1,n_2) goes to infinity in any direction, including the marginal ones. That was used to characterize the right limits and the essential spectrum of the corresponding Jacobi matrix on the binary tree.

The second preprint “Spectral theory of Jacobi matrices on trees whose coefficients are generated by multiple orthogonality“ with M. Yattselev finishes the program initiated in the original paper

A. Aptekarev, S. Denisov, and M. Yattselev, Self-adjoint Jacobi matrices on trees and multiple orthogonal polynomials, Trans. Amer. Math. Soc., Vol. 373, N2, 2020, 875-917

now published in Transactions of AMS. When two measures of orthogonality are involved, we study Jacobi matrixes generated by MOPs of the first and of the second types. Those of the second type give rise to a Jacobi matrix on the finite binary tree, which is self-adjoint in indefinite metric (it is sign-definite for Angelesco system and is non-sign-definite for Nikishin system). We find the spectrum and construct the basis of eigenvectors each of which can be written in terms of these MOPs. The analysis for MOPs of the first type is more involved since the associated Jacobi matrix is defined on the infinite binary tree. For Angesleco system, this Jacobi matrix is self-adjoint in the standard metric and we find the convenient decomposition of the Hilbert space into the orthogonal sum of cyclic subspaces. Each subspace is described by a generalized eigenvector which is written via the MOPs of the first type. The spectral measures of generators are found explicitly thus making the complete analysis of the spectral type possible. In short, this paper puts the connection between MOP and the operator theory on the solid ground. Unlike for one-dimensional theory, the feature of multi-dimensional case is that often times the theory of self-adjoint operators in indefinite metric (in Krein spaces) starts to play the role.

***********************************************************************

June 18, 2018. In the recent preprint with A. Aptekarev and M. Yattselev, we found the missing link between the spectral theory of self-adjoint operators and the theory of multiple orthogonal polynomials. Recall that given a measure on the real line with compact support, we can construct a sequence of orthonormal polynomials which satisfy three-term recurrence that defines one-sided Jacobi matrix. This matrix is actually a self-adjoint operator in \ell^2(Z^+) for which many standard quantities of operator theory (e.g., Green’s function, spectral measures, etc) can be computed through the measure we started with and the associated orthogonal polynomials. Conversely, given a bounded self-adjoint Jacobi matrix, we can uniquely find the measure of orthogonality that generates it. This correspondence proved to be very useful both in spectral theory and approximation theory (however, to my knowledge never played a crucial role in proving deeper analytical results). The multiple orthogonal polynomials (MOPs) can be of two types and they are defined given d measures through some orthogonality conditions (see the paper for details). These polynomials depend on multi-index \vec{n} of dimension d and satisfy recurrence relations on the integer lattice. It turns out that, to define the corresponding operator, one has to untwine  these recurrences to the rooted 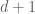d+1 homogeneous tree. The resulting operator is a self-adjoint Jacobi matrix which is defined on that tree. We obtained, among other things, the formulas connecting the Green’s function to MOPs and found its spatial asymptotics for analytic weights using matrix Riemann-Hilbert analysis. The usefulness of this connection is illustrated by, e.g., reproving some known results.

Confinement of the support of positive vorticity in 2D Euler evolution

March 30, 2018 in Uncategorized | Leave a comment

In the recent preprint (to appear in Comm. Math. Phys.) “On the growth of the support of positive vorticity for 2D Euler equation in an infinite cylinder”, Kyudong Choi and I obtained an upper bound for the diameter of the support of positive vorticity in the 2D Euler dynamics

\theta_t+u\cdot \nabla \theta=0, \quad \theta(x,y,0)=\theta_0(x,y).

We considered the problem on the infinite cylinder which is equivalent to 2\pi-periodic initial data in one direction. If one takes \theta_0 as nonnegative bounded function with compact support, then the weak solution exists globally in time. If d(t) denotes the diameter of its support, then the trivial bound reads

d(t)\leq C(1+t).

In the paper, we improve it to

d(t)\leq C(1+t)^{\frac 13} \log^2(2+t).

Our argument is based on controlling the sequence of specially chosen moments on the dyadic spatial scale. The crucial part of the argument was to exploit the uniform in time estimate on the first moment of vorticity. For the problem on the whole plain, similar results were obtained previously in the paper by Iftimie, Sideris, and Gamblin “On the evolution of compactly supported planar vorticity”. Our method is different from the one used previously in that it uses another conserved quantity and different set of moments.

The 2D Euler evolution in infinite cylinder is remarkable model because the kernel in the Biot-Savart law that expresses velocity u in terms of \theta has the exponentially decaying first component. That means two distant parts of vorticity are essentially decoupled. One would hope that this, along with conservation of horizontal center of mass, should yield much stronger bound on d(t), for example, d(t)\leq C_\epsilon(1+t)^\epsilon. This, however, seems difficult to achieve due to possible “diffusive dynamics” of \theta.

One possible interesting direction is to study the evolution of patch of vorticity in the active scalar equation when no conserved quantities are known but the kernel in the Biot-Savart law is short-range and has some basic symmetries. One would think that this should be enough to prove strong confinement results.

Szego theorem on the real line and Krein strings

November 15, 2017 in Szego theorem on the real line and Krein strings, Uncategorized | Leave a comment

Roman Bessonov and I just posted the paper “A spectral Szego theorem on the real line” on arxiv. You can also read it here. Given a probability measure \sigma on the unit circle, one can ask when the analytic polynomials are NOT dense in L^2(\sigma). The theorem of Szego claims that this is so iff any of the following conditions holds:

  • \int_{T}\log \sigma'd\theta>-\infty
  • The sequence of recurrence parameters \{a_n\} (or Schur parameters) of polynomials orthogonal with respect to \sigma belongs to \ell^2.

Given a measure on the real line \mu that satisfies normalization

\displaystyle \int_{R}\frac{d\mu(t)}{1+t^2}<\infty,

we can ask the question when the set of functions

\displaystyle  \int_0^\infty e^{itx}f(x)dx, f\in C^\infty_c(0,\infty)

is NOT dense in L^2(\mu). The answer is given by the theorem of Kolmogorov-Krein-Wiener: it is iff

\displaystyle \int_{R} \frac{\log \mu'}{1+t^2}dt>-\infty

However, the spectral characterization of this condition has been missing. In the paper, we consider the Krein string, – the “mother of all non-negative self-adjoint operators with simple spectrum”. It is given by the formal differential operator

\displaystyle S=-\frac{\partial}{\partial M} \left( \frac{\partial}{\partial t}\right)

where M is any non-decreasing function on R^+. The corresponding self-adjoint operator can be defined and its spectral measure \mu along with one additional real parameter determines M completely. In the paper, we characterize all strings M for which the logarithmic integral of \mu converges. This is done by proving analogous statement for diagonal De Branges canonical systems. The existence of the entropy is important for the prediction theory of stationary Gaussian processes with continuous time. It is likely that the obtained characterization will allow one to quantify some statements in this theory.

Wave operators for wave equation

July 4, 2017 in Uncategorized, Wave operators for wave equation | Leave a comment

In the recent preprint, I study the wave equation for the elliptic operator in divergence form. In \mathbb{R}^3 , define

H=-{\rm div }(1+V)\nabla,

where V oscillates and decays at infinity. More precisely, V={\rm div} \,Q where \|V\|<\infty, \|Q\|<\infty and the norm \|f\| is defined as

\|f\|=\left(\sum_{n=0}\max_{|x|\in [n,n+1]}|f|^2\right)^{1/2}.

I also assume \|V\|_\infty<1 to make sure that H is non-negative operator. The wave equation for H is

u_{tt}+Hu=0, \, u(x,0)=f_1,\, u_t(x,0)=f_2.

The main result of the paper states that the following wave operators

\lim_{t\to\pm \infty} e^{it\sqrt{H}}e^{-it\sqrt{-\Delta}}f=W^{\pm}f

exist for every f\in L^2(\mathbb{R}^3) and the limit is understood in L^2(\mathbb{R}^3) norm. The condition on V is optimal in some sense, i.e., the rate of decay is sharp and the oscillation is necessary if the potential is not short-range.

The proof is based on the analysis of the asymptotical behavior of the Green’s function G(x,y,k^2) where k\in \mathbb{C}^+ , y is fixed, and |x|\to\infty . The result about asymptotics is similar to that for the orthogonal polynomials on the circle in the Szego case. The main difference with the one-dimensional situation is that the resulting “Szego” function belongs to the vector-valued Hardy space. The operator e^{it\sqrt{H}} can be written through the resolvent (H-z)^{-1} by the contour integral and this is how the Green’s function enters the proof. The method is quite general and can be adapted to wave equations for the Schrodinger equation and other problems.

 

 

 

 

 

 

 

Stability of steady states for 2D Euler

May 19, 2016 in Stability of steady states for 2D Euler equation, Uncategorized | Leave a comment

In the recent preprint with Jen Beichman we considered the 2D Euler evolution on the tube S=\mathbb{R}\times \mathbb{T}. Each rectangle \Omega_L=[-L,L]\times\mathbb{T} is a steady state. We proved that if L is sufficiently large, then these steady states are stable for all time. For example, if one takes a patch \Omega such that |\Omega\Delta\Omega_L| is small, then the Euler evolution \Omega(t) of this patch will  have |\Omega(t)\Delta \Omega_L| small for arbitrary t. This result generalizes analogous statement for the stability of the disc on the plane (proved by Sideris-Vega). As Sideris and Vega, we used the method of V. Arnold. The idea of this method is to study the variational problem associated to the conserved quantities. In our case, these are

I_0=|\Omega(t)|,\,\, I_1=\int_{\Omega(t)} xdxdy,\,\, I_3=\int_{\Omega(t)}\psi dxdy

where \psi is a stream function given by \psi=\Delta^{-1}\chi_{\Omega(t)}. Then, we set up a variational problem with constraint

I_3\to\min,\,  I_2=0,\, I_1=4\pi L

We proved that the global minimizer is \Omega_L and if I_3(E) is close to the minimum value for some patch E, then E is close to \Omega_L in a weak topology. This essentially gives the required stability.

 

The V-states for the patch dynamics in active scalar equations

March 3, 2014 in The V-states for patch dynamics in active scalar equations, Uncategorized | 1 comment

March 3, 2014.

If one considers the 2d Euler equation of incompressible inviscid fluids on the plane in the vorticity form and takes the initial data as the characteristic function of a certain domain, then the Yudovich theory guarantees that the solution will exist globally and will be equal to the characteristic function of a time-dependent domain which is homeomorphic to the original one for all times. The numerical experiments dating back to the works of P. Saffman and Zabusky et al. indicate the existence of the centrally-symmetric V-states, i.e. a symmetric pair of patches that rotates with constant angular velocity around the origin without changing shape. If the distance between the patches in the pair equals to \lambda and \lambda>0, then the boundary of the V-state seems to be smooth. However, when \lambda=0, the both patches form a 90 degrees angle at the point of contact. The analytical proof for the existence of these V-states has never been obtained and this is an interesting problem. In the recent preprint, I considered the analogous equation with the cut-off. Loosely speaking, this corresponds to looking at the window around the origin where the contact of the patches is supposed to happen. Mathematically, the model with cut-off is important as it possesses the explicit singular solution: y_0(x)=|x| . Then, I addressed the problem of existence of the curve of smooth solutions that converge to y_0 in the uniform metric when the parameter \lambda\to 0.  Technically, this boils down to application of the implicit function theorem and is somewhat tedious. This technique might be important to better understand the mechanism of the merging and the sharp corner formation in the Euler dynamics. Another important problem is to prove that the merging in finite time is possible for the \alpha-model when \alpha<1 and is close to 1.

Multidimensional L^2 conjecture

February 19, 2012 in Multidimensional L^2 conjecture, Uncategorized | Leave a comment

May 2011. Consider H_0=-\Delta, x\in \mathbb{R}^d. Going on the Fourier side one can see that H_0 is equivalent to multiplication by |\omega|^2 and so the spectrum of H_0 is purely absolutely continuous (a.c.). From the physics perspective, the presence of a.c. spectrum is an indication that the wave propagation governed by

\displaystyle i\psi_t=H_0\psi

does have a transport effect (though without much specifics).

Perturb the Laplacian as follows H=H_0+V(x) where V(x) is potential and ask the question what is a minimal assumptions on V to guarantee that the a.c. spectrum is preserved. Make it a perturbation theory question, assume that V is in some weighted Lebesgue space L^p_w. Then, what are the critical p and w? In one-dimensional case, one answer is L^2(\mathbb{R}). This is a critical space. This result was proved for Schrodinger in a great paper by Deift and Killip but for Dirac it was known for at least half a century and dates back to the works by Mark Krein. Krein’s result on Dirac, however, is only a continuous analog of the classical results for polynomials orthogonal on the unit circle (Szego case).

For d>1, the conjecture by Barry Simon is that

\displaystyle \int_{\mathbb{R}^d} \frac{V^2(x)}{|x|^{d-1}+1}dx <\infty

is sufficient for the preservation of a.c. spectrum. Very little is known so far. Only the case of Schrodinger on the Cayley tree is well-understood. Take a rooted Cayley tree \mathbb{B} with the origin at O and assume that each vertex has exactly three neighbors while O has only two. Consider the Laplacian on \mathbb{B} defined at each point as the sum over the neighbors and then a simple calculation shows that the spectrum of H_0 is [-2\sqrt 2, 2\sqrt 2] and it is purely a.c. Then, perturb by V. The multidimensional L^2 result reads as follows. Consider all paths that go from O to infinity without self-intersections (rays). Put the probability measure on them by tossing a Bernoulli coin at each vertex. Then, the claim is that the a.c. spectrum contains the a.c. spectrum of unperturbed operator if with positive probability the potential V(X_n)\in \ell^2 where X_n denotes the path from the origin. There is more quantitative version, of course, which implies Simon’s conjecture if the Jensen inequality is applied. The condition we have here is more general and more physically appealing: it says that we only need enough directions were the potential is small for the particle to propagate.

For d>1, sparse or slowly decaying and oscillating potentials can be handled. If the potential does not oscillate, then the scattering process is quite complicated, it is governed by very intricate evolution equation (that captures semiclassical WKB correction as very special case). This evolution equation is poorly studied and much work is needed in this direction. Soft one-dimensional methods seem to be of little help.

In Euclidean case, what would be the analog of the probability space on the set of paths that escape to infinity? This question was addressed here. It turns out that there is a natural Ito’s stochastic equation that describes these paths. The statement we have is somewhat weak though. It says that the a.c. spectrum contains the positive half-line if V(X_t)\in L^1(\mathbb{R}^+) with positive probability and we can not yet replace summability by the square summability over the path X_t. Nevertheless, even this result gives rise to interesting questions like how one computes probabilities given by this Ito’s calculus? That conventionally can be reduced to the analysis of the corresponding potential theory and the modified harmonic measure. The potential theory one encounters in this case is somewhat in between elliptic and the parabolic one: on the large scale it is parabolic and on the small scale it is elliptic. The estimates on the harmonic measure in terms of the geometric properties of support can be found in my paper with Kupin.

___________________________________________________________________

May 2012. I recently finished writing a survey for the Nikolskii conference volume, it contains more details.